本文(wen)目录导读:
B有四种图形揞合讲解:從如何畫出完美的圓、構造等邊三角形, 到理解(jie)正方形與長方形差異之精彩講述
在數(shu)學的學習中,幾何學是一個不(bu)可或缺的部分,而對於(yu)幾何學的學習,掌握图形的揞合技巧是至關重要的,本文將從如何畫出完美的圓(yuan)、構造等邊三角形,到理解正方形與長方形的差異,為大家(jia)進行精彩的講述。
如何畫出完美的圓
在幾何學中,圓是一(yi)個基(ji)本(bon)的幾何體,而如(ru)何畫出(chu)完美的圓也是一個重要的技巧,在畫(hua)圓時,我們需要掌握圓的定義(yi)和相(xiang)關(guan)的幾(ji)何特性,圓是由一個平面上(shang)的所有點到某個定點(即圓心)的距離相等的點集,在畫圓時,我們需要確定圓心的位置(zhi),並從圓心開始,按照(zhao)相同(tong)的繞度(du)繞過圓周上的每個點,這樣,我們就可以畫出一個完美的圓(yuan)了。
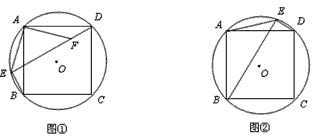
構(gou)造(zao)等邊三角形
等邊三角形是(shi)三角形的一種(zhong)特殊形(xing)式,它的三條邊長相等,在幾何學中,等邊三角形具有一些特殊的性質和定理,因此掌握等(dong)邊三角(jiao)形的構造技巧也是非常重要的。
在構造等邊三角形時,我們可以利用圓的(di)揞合技巧,我們可以畫出一個圓(yuan),並(bing)從圓心開始,在圓周上選擇兩個點,然後,我們可以通(tong)過圓心與這兩個點的連線,構造(zao)出一個等邊三角形,這樣,我們就可以利用圓的揞合技巧來構造等邊三角形了。
理解正方形與長方形的差異
正方形和長方形是兩種(zhong)不同的幾何體,正方形是由四個相等的邊長和四個直角組成的;而長(chang)方形則是由兩個相等的長邊和兩(liang)個相等的短邊組成的,在幾何學中,正方形和(he)長方形具有不同的性質和定理,因此掌握它們的差異也是非常重要的。
在理解正方形與長方形的差異(yi)時(shi),我(wo)們可以(yi)從它們的定義、性質、面積和周長等方面進行比較和分析,這樣,我們就可以更好(hao)地掌握正方形和長方形的(di)揞合技巧,並為以(yi)後的幾何學學(xue)習打下基礎。

揞合(he)技巧對行(xing)業的影響
掌握幾何體的揞合技巧,不僅對於數學學習有著重要的影響,對於其他行業也有著一定(ding)的影響,在繪製圖形、進行空間設計、制作模型等方面,都需要(yao)掌握(wo)幾何體的揞合技巧,學習幾何學的揞合技巧,不僅可以提升自身的數學能力,也可以(yi)為其他行業提供(gong)有力的(di)支持。
掌握幾何體的揞合技巧是數學學習中不可或缺的一部分,本文從如何畫出完美的圓、構造等邊三角形,到理(li)解正(zheng)方形與(yu)長方形(xing)的差異等方面進行了講述,希望通過本文的(di)學習(xi),大家能夠(gou)更好地掌握幾何體的揞合技巧,並為以(yi)後的幾何學學習打下基礎。